Quantum Computing

... from transistors to quantum supremacy

Slides by Nik Hartman. Originally for Nerd Nite YVR #37.

Quantum supremacy

• When a quantum computer can accomplish something a classical computer cannot.
• Likely to show up in your newsfeed in the next 1-5 years.

First -- Let's talk classical computers

All the computer hardware we know and love today is based on the semiconductor transistor .

Transistors = Semiconductor Junctions

Before we do calculations... let's learn to count

$2^2=4$	$2^1=2$	$2^0=1$	SUM
0	0	0	0
0	0	1	1
0	1	0	2
0	1	1	3
1	0	0	4
1	0	1	5
1	1	0	6
1	1	1	7

Transistors to logic gates (if-then statements)

AND-gate
A	B	OUTPUT
0	0	0
1	0	0
0	1	0
1	1	1

many possible logic gates can be created

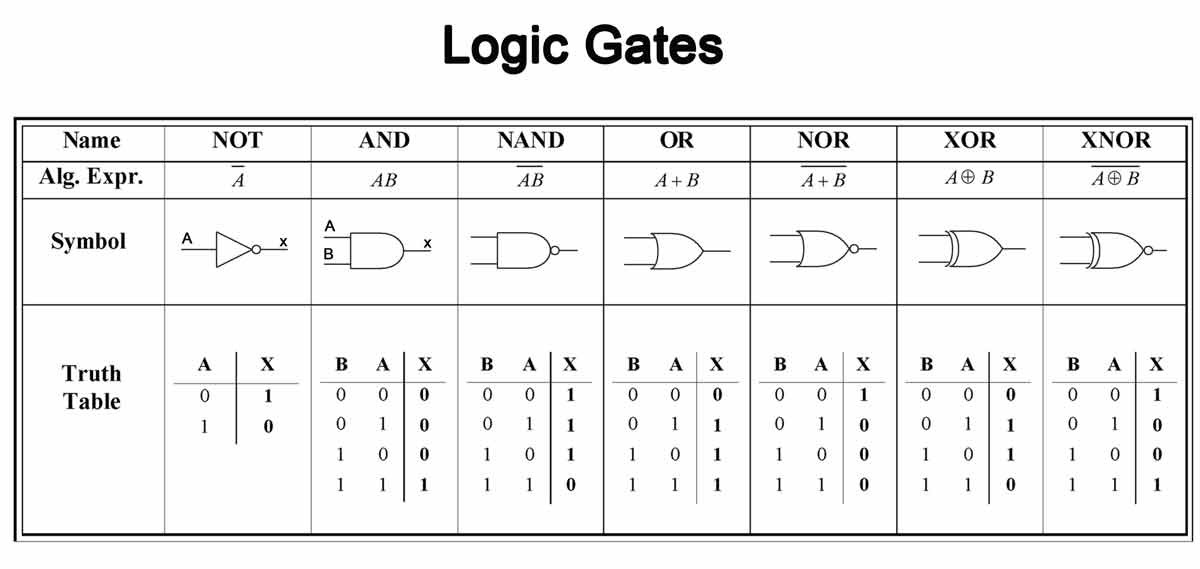
EXAMPLE: 2 + 3 = ??? (or 010 + 011 = ???)

2 + 3 = 5

but computers do more than add numbers...

• Many of the hardest computational problems are simulations of nature.
• Often we can be simplify and accept approximate results
• What about exact simulations of nature?
• To describe nature exactly we need quantum mechanics.

Why is simulating quantum mechanics difficult?

Superposition

A fundamental property of the very small world.

• The only results we can measure are $\uparrow$ or $\downarrow$
• Before measurement it can exist in a combination (superposition) of both states.

superposition = $a \cdot \downarrow + b \cdot \uparrow $

• $a$ and $b$ are the probabilities of measuring the atom pointing down or up

Superposition -- An Analogy*

superposition = $\frac{1}{2} \cdot LAMB + \frac{1}{2} \cdot LOBSTER $

• What happens when the waiter asks (measures) what you would like?
• Your uncertain order (superposition) collapses into a single decision.
• If this scenario could be recreated over and over -- 50% of the time you choose lamb, 50% lobster

* without any dead cats

more is different -- and may be impossible

• A system of N atoms has $2^N$ possible configurations
• $ 2 \cdot 2 \cdot 2 \ldots 2 \cdot 2 \cdot 2 = 2^N $
• Any simulation must keep track of all of these configurations to determine most probable measurement result
• Adding another atom doubles the processing power needed

ok.. let's double the processing power!

What do we get for all that power?

Simulate interactions between 45 atoms

Using current technology and all of the world's electricity, we can get to about 70 atoms.

Richard Feynman suggests a way out

If simulating quantum mechanics on a classical computer is too costly, build a quantum computer.

Transistors + Quantum Mechanics = quantum bits

A quantum processor needs more than one qubit

• Qubits can be combine to make more complicated superpositions
• Single atom superposition:
  $$superposition = a_0 \cdot \downarrow + a_1 \cdot \uparrow$$
• Many atoms forming a single superposition are entangled.
• Multiple (3) atom entangled superposition:
  $$superposition = a_0 \cdot \downarrow\downarrow\downarrow + a_1 \cdot \downarrow\downarrow\uparrow + a_2 \cdot \downarrow\uparrow\downarrow + a_3 \cdot \uparrow\downarrow\downarrow + \\ a_4 \cdot \downarrow\uparrow\uparrow + a_5 \cdot \uparrow\downarrow\uparrow + a_6 \cdot \uparrow\uparrow\downarrow + a_7 \cdot \uparrow\uparrow\uparrow$$
• We can perform logical gates (if-then statements) on these quantum bits!
• Connect quantum bits with a gates (if-then statements, e.g. AND, NAND, XOR, ...)
• We invented a quantum computer!

A sensibly sized simulation of nature

• Entangled state of N-qubits is a superposition of all $2^N$ configurations.
• $$superposition = a_0 \cdot \downarrow\downarrow\downarrow + a_1 \cdot \downarrow\downarrow\uparrow + a_2 \cdot \downarrow\uparrow\downarrow + a_3 \cdot \uparrow\downarrow\downarrow + \\ a_4 \cdot \downarrow\uparrow\uparrow + a_5 \cdot \uparrow\downarrow\uparrow + a_6 \cdot \uparrow\uparrow\downarrow + a_7 \cdot \uparrow\uparrow\uparrow$$
• Quantum computer needs only N qubits to simulate N quantum mechanical objects.
• About 50 qubits can do something impossible for a classical computer!

stay tuned for quantum supremacy!